El problema del sofá, un enigma matemático de casi 60 años de antigüedad, probablemente fue resuelto por un estudiante surcoreano como parte de su tesis en la Universidad de Michigan en Estados Unidos. Se puede leer en prepublicación desde el 2 de diciembre en el sitio web de ArXiv.
Todo el mundo ha experimentado la molestia de mover un sofá por un pasillo, una situación inmortalizada en la serie. Amigos durante una escena pasada la posteridad. Bueno, es muy posible que esta dificultad crucial para la humanidad (al menos para cualquiera que se esté embarcando en un movimiento) ya no lo sea.
Jineon Baek, investigador postdoctoral de la Universidad Yonsei de Seúl, hizo su tesis sobre este problema matemático en la Universidad de Michigan y propuso una solución. El 2 de diciembre, su tesis se publicó en línea como prepublicación (por lo tanto, aún no revisada por pares matemáticos) en el sitio ArXiv.
Un sofá particular, el de Gerver
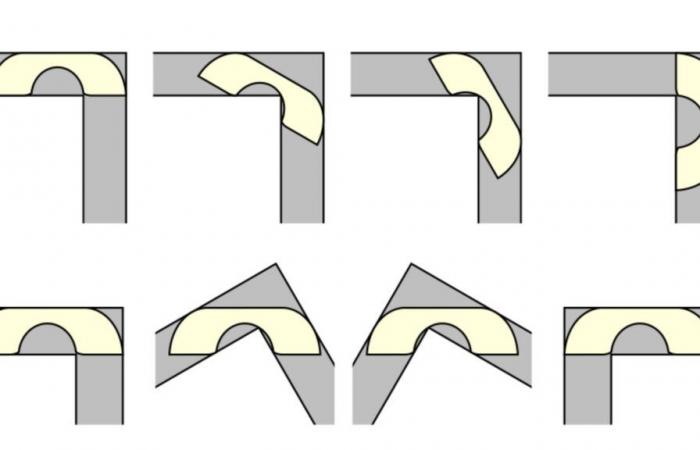
El problema del sofá, también llamado problema del sofá, data de 1966 y es fácilmente comprensible, incluso para los no matemáticos. Leo Moser, un matemático austríaco-canadiense, está tratando de encontrar la superficie más grande de un sofá que se pueda mover horizontalmente en un pasillo de una unidad de ancho y que tenga un ángulo recto.
Pero si el problema simplemente surge, su resolución es difícil. Se trata de un cálculo más complicado de lo que parece, porque hay que conseguir hacer coincidir la superficie correcta del mueble con el movimiento que debe realizar el sofá en el espacio, teniendo en cuenta las limitaciones (el ángulo recto y cada parte del pasillo). .
Anteriormente, con diferentes estudios se estableció que el área máxima se encontraba en el intervalo entre 2.2195 unidades y 2.37 unidades.
El límite inferior de este intervalo (por tanto 2,2195) fue demostrado en 1992 por el matemático Joseph Gerver, profesor de la Universidad de Rutgers, en Nueva Jersey (Estados Unidos). El profesor también había determinado una forma particular para este sofá: un cubo compuesto por un hueco semicircular y bordes redondeados.
El límite superior (2,37) fue encontrado mediante un método asistido por computadora en 2018 por Dan Romik y Yoav Kallus, dos matemáticos que trabajan en la Universidad de California en Davis y la Universidad de Santa Fe, Nuevo México, respectivamente.
La solución definitiva al problema del sofá.
Jineon Baek, para solucionar el problema, empezó con la forma del sofá desarrollado por Joseph Gerver. Después de cien páginas de demostración, finalmente llegó a la siguiente respuesta: en un pasillo de una unidad de ancho, la máxima superficie posible del sofá es efectivamente la que Gerver había encontrado inicialmente, es decir 2,2195 unidades. .
Su solución aún debe ser verificada por diferentes matemáticos, pero bien podría ser que, 58 años después de su formulación, este sea el fin de este problema matemático.