En matemáticas, ciertas conjeturas suscitan convicciones muy fuertes entre los especialistas; por ejemplo, pocos matemáticos piensan que la hipótesis de Riemann o la conjetura de Siracusa sean falsas. Sin embargo, a veces una afirmación que todo el mundo pensaba que era cierta resulta ser errónea. Esto es lo que ocurrió con la “conjetura de la litera”, en teoría de grafos: a principios de octubre de 2024, Nikita Gladkov e Igor Pak, de la Universidad de California en Los Ángeles, así como Aleksandr Zimin, del MIT (el Instituto de Massachusetts) of Technology), todos ellos en Estados Unidos, han publicado en Internet una prepublicación en la que presentan varios contraejemplos de una afirmación que, sin embargo, ha obtenido una amplia aceptación desde su primera formulación en 1985.
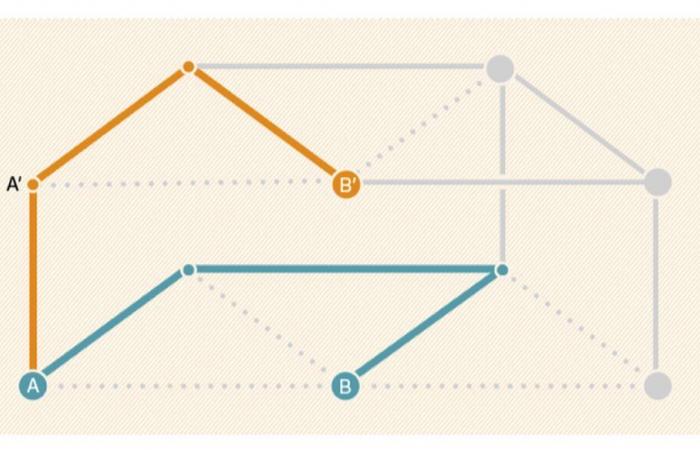
Considere un gráfico GRAMO conectado (es decir un conjunto de vértices unidos entre sí por aristas, formando una única estructura) y duplíquelo para obtener un segundo gráfico GRAMO’idéntico. Ahora elijamos un subconjunto de los vértices de GRAMOy conectar cada uno de ellos por una nueva arista al vértice correspondiente de GRAMO’. De esta manera, construimos un nuevo gráfico que se asemeja a una litera, cuya litera inferior es el gráfico GRAMOel que está en la parte superior del gráfico GRAMO’y las cantidades son estas aristas que unen vértices primos de GRAMO y GRAMO’. Ahora imagina que cada borde de esta “litera” desaparece con cierta probabilidad. pag. Como GRAMO estaba conectado (en una sola pieza), siempre era posible, en el gráfico inicial, unir dos vértices cualesquiera de GRAMO – digamos A y B – por un camino continuo de bordes de GRAMO. Como ciertas cumbres de GRAMO estaban conectados a los vértices correspondientes de GRAMO’y eso GRAMO’también estaba conectado, también era posible, en la litera inicial, conectar A en la cima de GRAMO’correspondiente a B – llamémoslo B’. Pero, ¿qué sucede una vez que se eliminan ciertos bordes al azar? La conjetura de 1985 establece que, en la litera final (después de la eliminación probabilística de los bordes), la probabilidad de que un camino se una A y B es mayor que la probabilidad de que un camino se una A y B’.
Al trabajar en esta conjetura, Nikita Gladkov y sus colegas se inspiraron en los resultados de Lawrence Hollom, un estudiante de doctorado de la Universidad de Cambridge, Inglaterra, que también estaba estudiando el problema, inicialmente para demostrar que la afirmación era correcta. Como el resultado se le resistía, se concentró en la misma pregunta trasladada a objetos un poco más “dóciles”. »: hipergrafos, una generalización de gráficos donde las aristas pueden conectar más de dos vértices. “Como no avanzaba mucho, comencé a buscar problemas similares en hipergrafías, pero más simples. Sin embargo, me di cuenta de que para que la conjetura de la litera fuera cierta, muchas otras afirmaciones más simples tenían que serlo también… y que al final iba a ser muy difícil garantizar que esas afirmaciones fueran siempre verificadas, todo al mismo tiempo. ¡al mismo tiempo! » Resultado: el investigador cambió de opinión y, en junio de 2024, presentó en una prepublicación un contraejemplo de la conjetura de la litera para los hipergráficos.
A partir de este trabajo, Nikita Gladkov, Igor Pak y Aleksandr Zimin lograron a su vez construir un contraejemplo de esta conjetura, esta vez para gráficos, en el caso en que la probabilidad de que desaparezcan las aristas valga la pena. pag = 1/2. “Nuestro contraejemplo es un gráfico GRAMO en 7.222 picos, dice Nikita Gladkov. Es enorme, pero ese tamaño se debe al hecho de que lo construimos a mano a partir del hipergráfico de Lawrence Hollom. ¡Por tanto, entendemos muy bien por qué no verifica la conjetura! » En este gigantesco contraejemplo, efectivamente hay dos vértices A y B del grafico GRAMO como la probabilidad de que un camino se una A y B en la litera, después de eliminar cada borde con una probabilidad de 1/2, es menor que la probabilidad de que un camino se una A y B’. Ridículamente más pequeño, es cierto: la diferencia de probabilidad es inferior a 10-4331. Pero más pequeño de todos modos.
Tenga en cuenta que, aún en el caso de que pag = 1/2, los investigadores identificaron un contraejemplo mucho más pequeño: un gráfico GRAMO en 82 picos. Pero esto último no se entiende tan bien: “No sabemos cómo prescindir de un ordenador para demostrar que se trata de un contraejemplo”, se lamenta Nikita Gladkov.
A Igor Pak le gusta decir que de una semana de investigación matemática es bueno dedicar seis días a pruebas y un día a contraejemplos. Nikita Gladkov está de acuerdo: “Quizás este episodio muestre que debemos ser más escépticos ante las conjeturas clásicas. Cuando se manipulan estructuras grandes y no muy rígidas, hay muchos grados de libertad: esto deja espacio para que sucedan cosas inesperadas y contraintuitivas. »
Descargue la versión PDF de este artículo.
(reservado para suscriptores digitales)